Mendefinisikan Pangkat Rasional Dengan Benar

Di dalam Matematika ada beberapa struktur yang perlu kita kita ketahui, ialah aksioma (postulat), teorema (dalil), pengertian pangkal, dan definisi. Kali ini kita akan membahas mengenai definsi. Di dalam mendefinisikan suatu istilah, kadang kita  kurang lengkap dalam memberikan suatu batasan. Misal definisi persmaan kuadrat adalah "Persamaan yang berbentuk  . Kadang-kadang kita lupa memberi batasan bahwa .

Sekarang perhatikan contoh berikut ini

Tampaknya terjadi kontradiksi (hasilnya tidak sama). Mengapa ini sampai terjadi? Hal ini karena kita kurang dalam memberikan batasan dalam mendefinisikan pangkat rasional. Perhatikan definisi pangkat rasional berikut ini!

Bila a bilangan real, m, n bilangan bulat positif, m dan n relatif prima maka didefinisikan:

m dan n relatif prima artinya m dan tidak mempunyai faktor persekutuan selain 1 atau dengan kata lain pangkat rasional 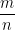  merupakan pecahan yang paling sederhana. Sekarang perhatikan pangkat rasional  , bilangan ini tidak relatif prima, karena 6 dan 2 mempunyai faktor persekutuan 3. Jadi  merupakan pengerjaan yang salah karena tidak sesuai dengan definisi. Batasan mengenai relatif prima antara m dan n inilah yang sering dilupakan dalam mendefinisikan pangkat rasional.

Dalam menurunkan suatu sifat dari pangkat rasional kadang di beberapa buku tidak memberikan batasan yang lengkap, bahkan ada buku yang memberika batasan yang salah. Salah satu sifat pangkat rasioanal adalah:
 ada buku yang memberikan batasan a bilangan real, m dan n bilangan rasional. Seharusnya batasan yang benar a bilangan real positif. Mari kita perhatikan kasus berikut:
Misal a = -2, m = 2, dan n = 1/2.
Kita hitung ruas kiri:

Sekarang kita hitung ruas kanan:

Ternyata hasilnya tidak sama (kontradiksi). Mengapa? Karena a negatif. Padahal batasannya a positif