 Kemarin saya sudah menulis tentang pertidaksamaan irasional. Sebagian langkah untuk menyelesaikan pertidaksamaan irasional adalah mengkuadratkan kedua ruas. Yang perlu diperhatikan adalah jangan sampai lupa memberi batasan (syarat) ketika mengkuadratkan kedua ruas. Berikut ini saya menulis lagi mengenai pengkuadratan kedua ruas baik pada persamaan irasional maupun pertidaksamaan irasional. Perhatikan contoh-contoh berikut:
Kemarin saya sudah menulis tentang pertidaksamaan irasional. Sebagian langkah untuk menyelesaikan pertidaksamaan irasional adalah mengkuadratkan kedua ruas. Yang perlu diperhatikan adalah jangan sampai lupa memberi batasan (syarat) ketika mengkuadratkan kedua ruas. Berikut ini saya menulis lagi mengenai pengkuadratan kedua ruas baik pada persamaan irasional maupun pertidaksamaan irasional. Perhatikan contoh-contoh berikut:Contoh 1
Selesaikan persamaan 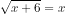 !
!
Penyelesaian:
Sebelum mengkuadratkan kedua ruas, harus diperhatikan batasannya.
x + 6 >= 0 ekuivalen dengan x >= -6.
Kuadratkan kedua ruas, maka persamaan menjadi
x + 6 = x2
x2 - x - 6 = 0
(x + 2)(x -3) = 0
x = - 2 atau x = 3
Keduanya memenuhi syarat karena keduanya >= -6. Namun masih harus kita cek keduanya dengan cara substitisikan ke dalam persamaan.
Untuk x = -2 didapat
Untuk x = 3 didapat
Yang harus diperhatikan dalam menyelesaikan persamaan irasional adalah menguji jawaban yang telah diperoleh.
Contoh 2
Selesaikan pertidaksamaan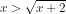 !
!
Penyelesaian:
Syarat di bawah tanda akar adalah x + 2 >= 0 ekuivalen dengan x >= -2
Syarat pengkuadratan adalah kedua ruas >= 0, ruas kanan pasti >= 0 (jadi tidak perlu diberi syarat). Ruas kiri x >= 0.
Kedua syarat, yaitu x >= -2 dan x >= 0 menjadi x >= 0
Kuadratkan kedua ruas, maka menjadi
Contoh 2
Selesaikan pertidaksamaan
Penyelesaian:
Syarat di bawah tanda akar adalah x + 2 >= 0 ekuivalen dengan x >= -2
Syarat pengkuadratan adalah kedua ruas >= 0, ruas kanan pasti >= 0 (jadi tidak perlu diberi syarat). Ruas kiri x >= 0.
Kedua syarat, yaitu x >= -2 dan x >= 0 menjadi x >= 0
Kuadratkan kedua ruas, maka menjadi
x2 > x + 2
x2- x - 2 > 0
(x + 1)(x - 2) > 0
x < -1 atau x > 2.
Karena syaratnya x >= 0 maka penyelesaiannya hanya x > 2.
Kesimpulan yang dapat kita ambil adalah jangan asal mengkuadratkan kedua ruas persamaan atau pertidaksamaan irasional. Perlu diperhatikan adalah pemberian syarat-syarat yang diperlukan.
0 komentar:
Posting Komentar